# Prefix --------------------------------------------------------------------------
# Remove all files from ls
rm(list = ls())
# Loading packages
require(survival)
require(rootSolve)
require(dplyr)
require(tibble)
require(data.table)
# Loading dataset -----------------------------------------------------------------
#Reading the example data set lung from the survival package
lung <- as.data.frame(survival::lung)
#Recode dichotomous vairables
lung$female <- ifelse(lung$sex == 2, 1, 0)
lung$status_n <- ifelse(lung$status == 2, 1, 0)
# Define model data for futher use
model_data <- lung[, c("status_n", "time", "female", "age")] |>
rename("d" = status_n,
"t" = time,
"x1" = female,
"x2" = age)Some time ago, I felt that I came across the term M-estimation more often when reading articles on causal inference. Hence, it has been due time to learn a bit more about what M-estimation is about. This summer I was lucky enough to take a very nice and useful introductory workshop on M-estimation titled “The ABC of M-Estimation” given by Paul Zivich, Rachael Ross, and Bonnie Shook-Sa. The workshop was given as a pre-conference course at this year’s annual SER conference. As I understood, this was not the last time the course will be given. So check out next year’s program of the SER meeting, if you want to learn more. I can highly recommend this course. They also wrote a nice introductory article on M-estimation, which was published in the International Journal of Epidemiology.
But let’s get our hands dirty and try to dive a little into what M-estimation is about! In this blog post I’ll talk you through (1) how to use M-estimation for estimating a Poisson model and (2) how to predict survival probabilities with accompanying confidence intervals from it. This post builds upon a previous post on using maximum likelihood estimation (MLE) for estimating a Poisson model. So, if you haven’t read the blog post yet, I would recommend you to take a look at it.
Before we can start applying M-estimation to some data, we need to go through some data preparation and a short theoretical background on M-estimation.
Data Set Up
This blog post will use the survival::lung dataset, which includes information on 228 patients diagnosed with advanced lung cancer. As an example, we will take a look at sex differences in survival in this patient group. If you want to know more about the dataset, you can take a look at the original publication. The original dataset used a 1/2 coding for binary variables. So let’s change this to 0/1. Before we start, we also need to load all the packages, that we will need for this session.
M-Estimation of a Regular Poisson Model
In the previous blog post, we fitted a Poisson model using age and sex as predictors of survival. The idea of this blog post is to reproduce that analysis using M-estimation instead of MLE. Before we can dive into the estimation of our models we need to go through some math in order to be able to set up our estimation equation.
Let’s assume we have a dataset which includes some observed data \(O\) for \(i=1, ..., n\) individuals. In general, a M-estimate can be defined as an estimate \(\theta\) that minimises our estimating function \(\rho(\cdot)\) with regards to \(\theta\):
\[ \hat{\theta} = \arg \min_\theta \bigg[ \sum_{i=1}^n \rho(O_i, \theta) \bigg], \]
where \(\rho(\cdot)\) is a function of the observed data and a model parameter. The estimating function is a function that links our model parameter to the observed data. Hence, we first need to define a model for the observed data. In the example at hand we would like to use a Poisson model to model the survival function of individuals included in the example dataset. Note that we can also estimate models with multiple parameters by stacking their estimating functions together, i.e., we need to find a set of estimates \(\theta\) that minimises all estimating functions. However, we can not only estimate parameters of the same model, but we can also stack different models together using M-estimation and estimate them simultaneously. For instance, if we want to estimate an IPW weighted Poisson model we both need to estimate our structural model and the exposure model for estimating the weights.
But to get started let’s just estimate a simple Poisson model. As a first step, we need to define its log-likelihood function. The survival function for a common Poisson model with a constant hazard function can be defined as
\[ S(t) = \exp(-\lambda t) \]
with \(\lambda = \exp(\beta_0 + \beta_1 x_1 + \beta_2 x_2),\)
where \(x_1\) is a indicator variable for the patient’s sex (0=male/1=female) and \(x_2\) is continuous age at lung cancer diagnosis. Based on the survival function and the hazard function, we can define the likelihood function of our model. The general likelihood for right censored survival data is defined as:
\[ L(\theta|d, t, \mathbf{x}) = \prod_{i=1}^n h(\mathbf{x}_i)^{d_i} S(t_i, \mathbf{x}_i). \]
Taking the log gives us the log likelihood function denoted \(\ell(\cdot)\):
\[ \ell(\theta|d, t, \mathbf{x}) = \sum_{i=1}^n d_i \log[h(\mathbf{x}_i)] + \log[S(t_i, \mathbf{x}_i)]. \]
If we now plug in our hazard and survival function in to this function, we get the log-likelihood function for our Poisson model.
\[ \ell(\theta|d, t, \mathbf{x}) = \sum_{i=1}^n d_i \mathbf{\beta}'\mathbf{x}_i - \exp(\mathbf{\beta}'\mathbf{x}_i) t_i \]
For estimating our model using M-estimation, we need to get the first partial derivatives of our log likelihood function with regards to the function parameters \(\mathbf{\beta}\), because we are interested in finding an estimate \(\theta\) that maximises our estimating function and the maximum of a function can be found by finding the root of its first derivative. Using the chain rule we get the following general form of the partial derivative of our log likelihood function.
\[ \frac{\partial}{\partial x_j} \ell(\theta|d, t, \mathbf{x}) = \sum_{i=1}^n d_i x_{ij} - \exp(\mathbf{\beta_j}x_{ij}) x_{ij} \]
However, for our estimating equation, we need to get the Jacobian (\(\triangledown\)) for our full log-likelihood, i.e., a vector of partial derivatives with regards to all parameters in the likelihood function. A general form of the Jacobian for the likelihood function of a Poisson model with \(j\) parameters can be defined as:
\[ \begin{split} \triangledown \ell(\theta|d, t, \mathbf{x}) & = \begin{bmatrix} \frac{\partial}{\partial \beta_0} \ell(\theta|d, t, \mathbf{x}) \\ \frac{\partial}{\partial \beta_1} \ell(\theta|d, t, \mathbf{x}) \\ \vdots \\ \frac{\partial}{\partial \beta_j} \ell_i(\theta|d, t, \mathbf{x}) \end{bmatrix} \\ & \\ & = \begin{bmatrix} \sum_{i=1}^n d_i - \exp(\beta_0)t_i \\ \sum_{i=1}^n d_i x_{1i} - \exp(\beta_1x_{1i})t_i \\ \vdots \\ \sum_{i=1}^n d_i x_{ji} - \exp(\beta_1x_{ji})t_i \\ \end{bmatrix} \end{split} \]
Now, having all partial derivatives in place, we can define our estimating function, which is the inner part of our estimating equation, i.e., \(\rho(O_i, \theta)\).
# Define estimating functions
ef1 <- \(O, theta) O$d * 1 - exp(cbind(1, O$x1, O$x2) %*% theta) * O$t * 1
ef2 <- \(O, theta) O$d * O$x1 - exp(cbind(1, O$x1, O$x2) %*% theta) * O$t * O$x1
ef3 <- \(O, theta) O$d * O$x2 - exp(cbind(1, O$x1, O$x2) %*% theta) * O$t * O$x2
# Combine all estimating function into one function
estimating_function <- function(O, theta){
cbind(ef1(O, theta),
ef2(O, theta),
ef3(O, theta))
}Next, we need to define the estimating equation, which is the sum of the estimating function over all observations \(i\), for a vector of parameters \(\theta\):
\[ \sum_{i=1}^n \rho(O_i, \theta) \]
estimating_equation <- function(par){
value = estimating_function(O = model_data,
theta = par)
colSums(value)
}Finally, we need to find the root of our estimating equation with regards to \(\theta\).
m_estimate <- rootSolve::multiroot(f = estimating_equation,
start = c(0,0,0))
data.frame(label = paste("beta", 0:2),
est = exp(m_estimate$root)) label est
1 beta 0 0.001069455
2 beta 1 0.618205147
3 beta 2 1.015741321Obtaining Confidence Intervals for our Estimates
There we go! We now fitted our Poisson regression model using M-estimation. Based on the results, we can see that females have a 39% lower hazard rate of death compared to males and that the hazard rate of death increases with 1.6% for each one year increase in age. However, we most likely would also be interested in getting some confidence intervals around our point estimates so that we can assess the uncertainty of our estimates. For this we can estimate the standard error and subsequent confidence intervals for our estimates using the Sandwich Variance estimator:
\[ \text{cov}(\hat{\theta}) = B(\hat{\theta}) ^{-1} F(\hat{\theta}) \big(B(\hat{\theta}) ^{-1}\big)^T \]
where \(B(\cdot)\) and \(F(\cdot)\) is the bread and filling matrix, respectively. Let’s start by baking the bread. The bread matrix can be estimated as the mean of the negative partial derivatives of our estimating function across all observations:
\[ B(\hat{\theta}) = \frac{1}{n} \sum_{i=1}^n \bigg[ -\rho'(O_i, \hat{\theta}) \bigg] \]
Let’s get the partial derivatives of each of the three estimating functions. For this, we will use the numerical approximation procedure implemented in the numDeriv::jacobian() function.
# Sum of partial derivatives of the estimating functions 1 to 3
ef1_prime <- numDeriv::jacobian(func = ef1,
x = m_estimate$root,
O = model_data) |>
colSums()
ef2_prime <- numDeriv::jacobian(func = ef2,
x = m_estimate$root,
O = model_data) |>
colSums()
ef3_prime <- numDeriv::jacobian(func = ef3,
x = m_estimate$root,
O = model_data) |>
colSums()Now we can compose our bread matrix based on the partial derivatives.
# Combine partial derivatives to bread matrix
bread <- matrix(c(-ef1_prime,
-ef2_prime,
-ef3_prime),
nrow = 3) / nrow(model_data)Once we have have the bread, we can continue with the filling, which is the average of the dot-product of our estimating function across all observations:
\[ F(\hat{\theta}) = \frac{1}{n} \sum_{i=1}^n \bigg[ \rho(O_i, \hat{\theta})^T \boldsymbol{\cdot} \rho(O_i, \hat{\theta}) \bigg] \]
value_ef <- estimating_function(m_estimate$root,
O = model_data)
filling <- (t(value_ef) %*% value_ef) / nrow(lung)Now that we the bread and the filling, we can get an estimate of the Sandwich variance and subsequently the Wald type confidence interval:
\[ \hat{\theta} \pm z_{\alpha/2} \sqrt{\frac{\text{Var}(\hat{\theta})}{n}} \]
covar <- solve(bread) %*% filling %*% t(solve(bread))
se <- sqrt(diag(covar) / nrow(lung))
data.frame(label = paste("beta", 0:2),
est = exp(m_estimate$root),
lci = exp(m_estimate$root - 1.96 * se),
uci = exp(m_estimate$root + 1.96 * se)) label est lci uci
1 beta 0 0.001069455 0.0003885294 0.002943749
2 beta 1 0.618205147 0.4710643248 0.811306616
3 beta 2 1.015741321 0.9997622104 1.031975823Obtaining Confidence Intervals for the Survival Function
However, quite often one is not only interested in the estimates itself, but also in transformations of these estimates, e.g., the survival function:
\[ g = S(t|x) = \exp[-\exp(\beta x) t] \]
There are two ways of estimating the survival function in this situation. The first option is to use the delta method for obtaining confidence intervals around our transformed estimates, i.e., the probability of surviving until a certain time point. The other option is to estimate the quantity of interest inside the M-estimation procedure. We can just add the survival probability at different time points to the estimating functions. However, I would usually prefer the first option as I kind of like to first fit the main model and then, in a second step, obtain different quantities that I’m interested in based on the model. So let’s get started with obtaining confidence interval for the survival function using the delta method.
We can also use the Sandwich variance estimator for estimating the variance of the survival function. For this we need the partial derivative of our transformation function \(g(\theta)\), which in our case is the survival function, with regards to our estimates \(\beta\). The variance estimator is then defined as
\[ \text{cov}[g(\theta)] \approx g'(\theta) \boldsymbol{\cdot} B(\theta)^{-1} \boldsymbol{\cdot} g'(\theta) \]
with the derivative of the survival function being
\[ \frac{\partial}{\partial \beta_i}g = \exp[-\exp(\beta x) t] -\exp[\beta x] t x_i. \]
Based on these function we can write our own small delta method function in R.
# Create own delta method function
delta_method <- function(x, t,bread, g, gprime){
g <- do.call(g, list(x = x, t = t))
gprime <- vapply(gprime, do.call,
FUN.VALUE = double(1),
args = list(x = x, t = t))
cov <- gprime %*% solve(bread) %*% gprime
se <- sqrt(diag(cov) / nrow(lung))
data.frame(est = g,
lci = g - 1.96 * se,
uci = g + 1.96 * se)
}Using this general function we can then, for instance, estimate a confidence interval for the probability of surviving more than 1 000 days in males and with lung cancer that have been 60 years at the date of their diagnosis.
# Get estimates (theta hat)
est <- m_estimate$root
# Use delta method function to get the survival probability of females
females <- delta_method(
x = c(1, 1, 60),
t = 1000,
bread = bread,
g = \(x, t) exp(-exp(x %*% est) * t),
gprime = list(\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[1]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[2]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[3]] * t)
)
# Use delta method function to get the survival probability of males
males <- delta_method(
x = c(1, 0, 60),
t = 1000,
bread = bread,
g = \(x, t) exp(-exp(x %*% est) * t),
gprime = list(\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[1]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[2]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[3]] * t)
)
# Output results
rbind(cbind(sex = "Females", females),
cbind(sex = "Males" , males)) sex est lci uci
1 Females 0.18495380 0.09981281 0.2700948
2 Males 0.06522466 0.03023816 0.1002111However, most likely we will not only be interested in getting a single survival probability but rather a survival function with accompanying confidence intervals. This can also easily be done with a loop over the time argument in our delta method function.
# Creating the data for the plot --------------------------------------------------
# Looping over time
survival <- lapply(seq(0, 1000, length = 300), \(i){
delta_method(
x = c(1, 1, 60),
t = i,
bread = bread,
g = \(x, t) exp(-exp(x %*% est) * t),
gprime = list(\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[1]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[2]] * t,
\(x, t) exp(-exp(x %*% est) * t) * -exp(x %*% est) * x[[3]] * t)
)
# Combining the output in a single data.frame
}) |> rbindlist()
# Adding a time variable to the data.frame
survival$t <- seq(0, 1000, length = 300)
# Plotting ------------------------------------------------------------------------
# Open new plot device
plot.new()
# Define plot windows
plot.window(xlim = c(0, 1000),
ylim = c(0, 1))
axis(1)
axis(2)
# Add CIs
polygon(c(survival$t, rev(survival$t)),
c(survival$lci, rev(survival$uci)),
border = NA,
col = "grey")
# Add point esitmates
lines(survival$t,
survival$est)
# Annotate plot
title(x = "Days After Lung Cancer Diagnosis",
y = "Survival Probability")
title(main = "Survival of Female Lungcancer Patients Aged 60 at Diagnosis",
adj = 0)
legend(0, 0.2,
legend = "95% CI",
fill = "gray")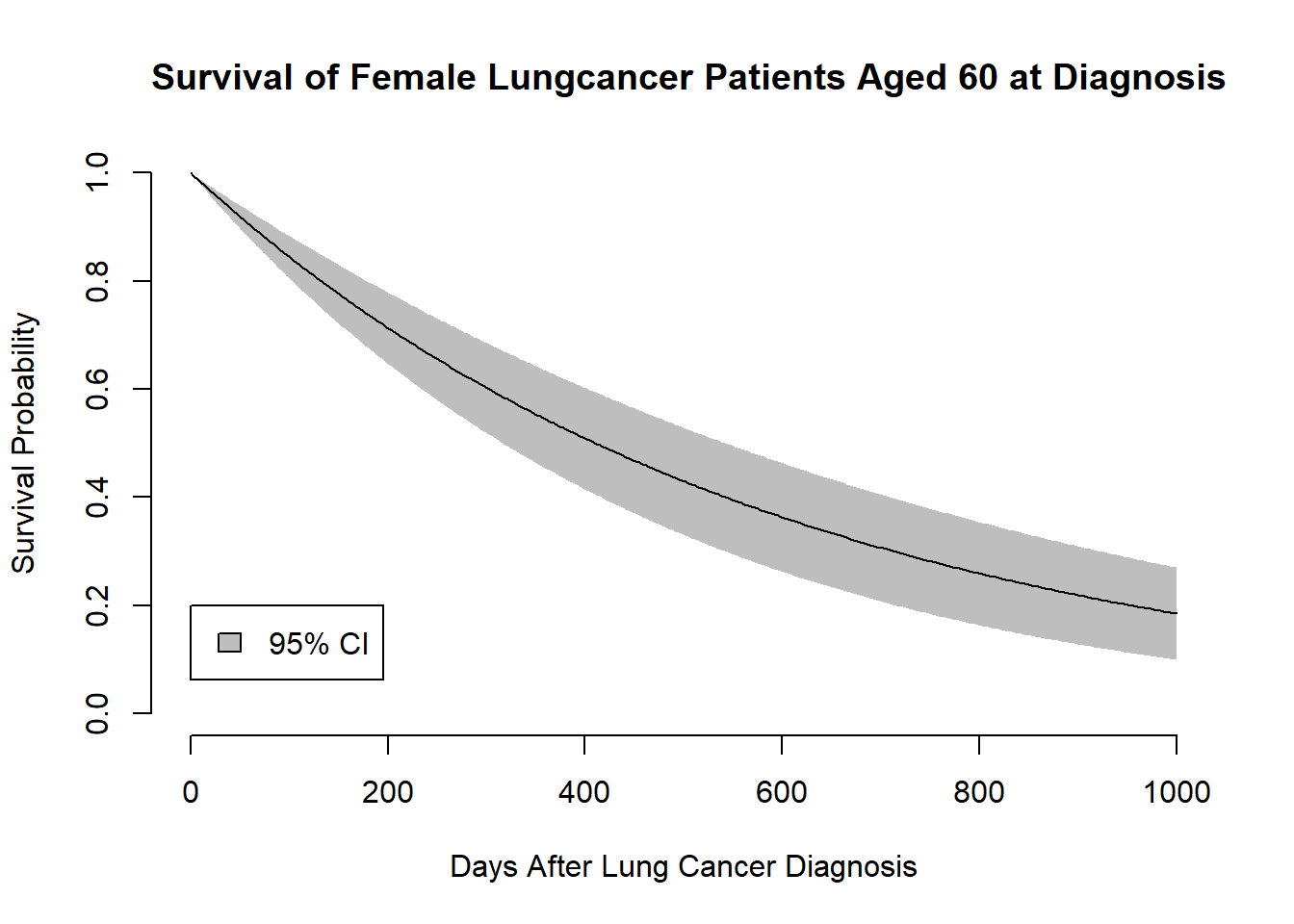
Here we go! We now managed to plot a survival function together with accompanying confidence intervals using M-estimation. You might wonder now why we did all this, if we could have gotten the same result using our standard glm() function? Obviously, we could have obtained this result with a standard likelihood based method, but I think this a nice starting point for diving deeper into M-estimation. The main advantage of M-estimation is that it nicely generalises to stacking a whole bunch of models that depend on each other in one estimating equation. This comes in handy if we, for instance, want to use IPW. Using M-estimation we can fit our main model of interest and the model for obtaining the weights at the same time. Through this approach our standard errors are also going to be automatically adjusted for the uncertainty arising from the model that we use for estimating our weights. I think that is pretty neat! However, that will be the topic of a follow-up post.